It is the eve of a brand new school year. Once again I will be requiring my students to reflect on their learning and themselves through the use of a blog. Each year I plan to blog along with them but I end up not doing it due to *insert excuse here*. I could fill that in with dozens of things that I have said over the years. But my hypocrisy is there staring me in the face. I spend so much time convincing them that reflection is maybe the greatest of the IB learner profile traits and yet I am not doing it myself. Well I do, but not in a meaningful way that I can look back on and track my growth. So I am making a new commitment to reflecting on my craft. When I was actively blogging I found it to be a very cathartic experience. I hope to recapture some of that feeling agian as I embark on 20th year in the classroom.
My thoughts about the importance of the IB learner trait of reflection:
It is the most important of the traits because without it you are not a learner. If you do not reflect on what you have done or ways you could have done it differently then how can you possibly improve? It is through reflection that we can measure our growth. Without reflection we just simply exist. Without honest reflection we can't get better. This year I will strive to do this alongside my students.
Sunday, August 26, 2018
Sunday, July 17, 2016
Unit 2 Work Product - 2016 E&M Modeling Instruction Workshop
'*In every modeling workshop there seems to be that moment when your brain explodes in a sudden clarity of understanding. This is that unit for me. This was the area I was weakest in understanding and just went through the motions with my students. The sad thing is I thought I understood it well enough. I definitely did not. On with the show.
Day 4 began with Don doing a bit of a review on proportional reasoning using the equation we derived on Day 3. An important bit of language was added to our vocabulary. If the distance doubled between to charges what happens to the force? Rather than saying it quarters, or it goes down by a fourth he asked us to use the following phrase: It decreases (or increases) by a factor of #. Where the # gets replaced with an integer. So if the distance doubles, the force decreases by a factor of 4. If the distance triples, the force decreases by a factor of 9. Half the distance? The force increases by a factor of 4. He also used the graph from our lab to reiterate this relationship that was very helpful visually.
He then brought our attention back to the fact that the Coulomb's Law and the Universal Law of Gravitation were so similar. We have been using this concept of gravitational field strength in our class for some time now. But haven't really talked much about them. The gravitational field of the earth is what gives an object weight. It pulls roughly 10N for every 1kg. If I double the mass, I double the force. This happens with charged objects too. So in this way we can think of charged objects of having an electric field. Since our units for grav. field are N/kg an analogous idea for charges would be the N/C. If I double the amount of charges the force increases by a factor of 2. Grav force can be calculated using the formula F=mg. Elec. force can be calculated using the equation F=qE. Since forces are a vector component, one of the variables on the other side of the equation must be a vector too. Mass can't be, and charges have pos. and neg. but it doesn't indicate direction of anything so we concluded that fields must have direction. Gravity fields are easy, they only pull one way so the earth's gravitational field points straight down. But we have different charges for electric fields so how will that work? Convention time! Evidently it was decided long ago that we will work with positive charges when determining the forces on charges. So the E. field points in the direction that a force would act on a positive charge due to the field.
So we came up with 2 rules about drawing electric field lines before we did some problems.
1. lines are drown in the direction of the force on a charge placed in the field.
2. closer spacing = stronger force.
As you move away from the center charge the lines get farther apart so force decreases.
If we have two long oppositely charged plates it forms a relatively constant electric field in between the plates. We know this because the field lines would all be equally spaced and parallel to each other. (It breaks down around the edges though so stick to the middle!)
We then reviewed energy and the fact that energy can be:
1. Stored
2. Transferred
3. Conserved
And since we can't see energy we have to classify it by the way that we observe it. (Kinetic (motion), Grav. (height), elastic (stretch/compression), heat (temp)) So what about electrical? We discussed it using an eraser in the gravitational field. When you lift the eraser does the eraser itself have more energy? The discussion led to that the energy is stored in the field itself. I don't know how to feel about that. Stuff we can't see is stored in something that is not really an object that we made up to explain the idea of things affecting other things at a distance. I don't like when we just have to accept something at face value but I don't see a way to come up with this idea other than how we did it. Another thing to keep thinking about.
We introduced the idea of gravitational potential and electrical potential. It is sort of like field strength for energy. Field strength was the force per unit of mass/charge, potential is the energy per unit of mass/charge. I think this is a particularly difficult idea just because it is something that really never gets used in normal conversation other than with batteries. Let's be honest, very few people understand what potential means with batteries either. It is just a word that is used with very little context or understanding around it. We began talking about potential using contour maps and dealing with the grav. field. Potential can be seen as a hill. The steeper the hill the stronger the localized field is. The taller the hill, the more potential there is. It was easy to wrap our head around because most of us had seem something like this before. Electrical equipotentials were a bit more difficult. We have opposite charges now.
At this point we did "the lab". I did not realize at the time how important this lab was, but we came back to it the rest of the workshop. Super important for our understanding. We placed two iron bars in a baking dish with a bit of water in it. We then connected them to a DC power source and used our potential-o-meters to measure the electrical potential at about a billion places. (Took forever!) we then graphed it using plot.ly to get a graph that looked just like a hill!
We had noticed that the hill looked like it was constant in its steepness for the majority of it. We concluded that must be the field strength value. Some groups used different voltages on their power supplies and got different slopes. Some used less distance between the plates and got the same result. We realized that if we moved the bars closer the hill would get steeper because the top and bottom had to stay the same. This connected back to our contour maps. When equipotential lines are close the hill is steep!
We then used a phet simulator to see how this worked with point charges instead of plates. The hills did not seem to be constant around point charges. They looked more like this:
The valley is caused by a negative charge as all positive charges would roll downhill towards it. Note that the hills change steepness as they get away from the charge. This goes back to the inverse square between distance and force on field strength. Interestingly, the inverse square thing doesn't seem to apply to the charged plates. We talked about this and the charges push on each other and pull on each other and based on superposition the forces stay pretty much equal. As you get farther from one plate you get closer to the other plate so it all stays constant.
Anyway, things were going very smoothly until we hit problem 11.
This problem made my brain weak. At first glance it looks EXACTLY LIKE THE LAB WE DID!!!! So my lab group breezed through it. Then Don and Laura kept coming by and reminding us that they were not hooked up to a power supply in the problem.
Us: Yeah. We get it. (don't change anything because we are so amazingly right)
Them: But the power supply was keeping the potential constant.
Us: Yeah. Cool. No charges can leave or enter so.... We're good!
Them: Really?
Us: Yes?
Them: Really really?
Us: Look energy is increasing since the plates are being pulled away right? So the field strength should get smaller and the distance increases and so the potential stays the same. We. Are. Good! You are not going to get us with your Jedi Mind Tricks!
(They go away) Us in our group: Ok. Why do they keep asking us this. Are we doing something wrong? Potential has to be the same right? No charges can move! When plates move away we know the field gets smaller we saw it! So what could we be doing wrong?
Eventually we got back in a group and discussed this problem.
Laura brought up this idea. If a charge is very close to one plate, pretty much only the charge next to it is pushing it away. All of the others are pushing on an oblique angle to it. Their forces balance out and so the charge gets pushed straight out from the plate. As the charge moves away the force from charge 3 gets reduced at the inverse square rate but here is where my mind exploded. At this point all of the charges around it have a greater effect because the angle they push at is much closer to 90! If you imagine the plate to be a huge wall (from a single charge perspective), the area of charges increases as a square to the distance! Yes, the one charge is less but the others start to help out more and so the force ends up being constant! Holy crap this changes everything! As the plates in question 11 separate the FIELD STAYS THE SAME!!!!!!!!! Energy goes up proportional to the distance moved. Since energy is equal to qEd and elec potential(V) is energy/q then Ee=qV. I can't believe we didn't see this before! If charge is not changing but energy is increasing, the potential CAN'T BE CONSTANT!!!!
Sorry for all the shouting. It was a very big moment for me in this unit.
Once we had this background set we were given these large blue cylinders that we were told were energy storage devices. (Later we learned they were called capacitors) A capacitor is basically two really big parallel plates rolled up into a smaller space but we could move the charges from one plate to another using a battery or a generator. (Note: This is not charging it! The device is still neutrally charged. Charges have just been moved from one plate to the other. We called this energized.)
There were various capacitors and we did a lab seeing how much energy was stored in each type. We found that as we increased the potential the energy increased as a square of the the change in the potential. The coefficient we labeled as 1/2 the capacitance. We then did a phet sim on capacitors to determine what things affect the capacitance. We also looked at using multiple capacitors. If we hooked them up in a straight line energy for each added capacitor went down! When we hooked them where one side was connected to one terminal of the battery and the other terminal to the other side (what we would later know as parallel) the graph of energy per capacitor added was linear! Crazy! As we thought about it it made some sense based on what we had done with the phet sim. Adding capacitors in parallel was like increasing the area of the plate which we saw had a direct relationship with energy. 2 capacitors = twice the area. For the one in series, the total potential was the same for all capacitors in a line so if there were 2 capacitors, each one only stored half the energy.
Day 4 began with Don doing a bit of a review on proportional reasoning using the equation we derived on Day 3. An important bit of language was added to our vocabulary. If the distance doubled between to charges what happens to the force? Rather than saying it quarters, or it goes down by a fourth he asked us to use the following phrase: It decreases (or increases) by a factor of #. Where the # gets replaced with an integer. So if the distance doubles, the force decreases by a factor of 4. If the distance triples, the force decreases by a factor of 9. Half the distance? The force increases by a factor of 4. He also used the graph from our lab to reiterate this relationship that was very helpful visually.
He then brought our attention back to the fact that the Coulomb's Law and the Universal Law of Gravitation were so similar. We have been using this concept of gravitational field strength in our class for some time now. But haven't really talked much about them. The gravitational field of the earth is what gives an object weight. It pulls roughly 10N for every 1kg. If I double the mass, I double the force. This happens with charged objects too. So in this way we can think of charged objects of having an electric field. Since our units for grav. field are N/kg an analogous idea for charges would be the N/C. If I double the amount of charges the force increases by a factor of 2. Grav force can be calculated using the formula F=mg. Elec. force can be calculated using the equation F=qE. Since forces are a vector component, one of the variables on the other side of the equation must be a vector too. Mass can't be, and charges have pos. and neg. but it doesn't indicate direction of anything so we concluded that fields must have direction. Gravity fields are easy, they only pull one way so the earth's gravitational field points straight down. But we have different charges for electric fields so how will that work? Convention time! Evidently it was decided long ago that we will work with positive charges when determining the forces on charges. So the E. field points in the direction that a force would act on a positive charge due to the field.
So we came up with 2 rules about drawing electric field lines before we did some problems.
1. lines are drown in the direction of the force on a charge placed in the field.
2. closer spacing = stronger force.
As you move away from the center charge the lines get farther apart so force decreases.
If we have two long oppositely charged plates it forms a relatively constant electric field in between the plates. We know this because the field lines would all be equally spaced and parallel to each other. (It breaks down around the edges though so stick to the middle!)
We then reviewed energy and the fact that energy can be:
1. Stored
2. Transferred
3. Conserved
And since we can't see energy we have to classify it by the way that we observe it. (Kinetic (motion), Grav. (height), elastic (stretch/compression), heat (temp)) So what about electrical? We discussed it using an eraser in the gravitational field. When you lift the eraser does the eraser itself have more energy? The discussion led to that the energy is stored in the field itself. I don't know how to feel about that. Stuff we can't see is stored in something that is not really an object that we made up to explain the idea of things affecting other things at a distance. I don't like when we just have to accept something at face value but I don't see a way to come up with this idea other than how we did it. Another thing to keep thinking about.
We introduced the idea of gravitational potential and electrical potential. It is sort of like field strength for energy. Field strength was the force per unit of mass/charge, potential is the energy per unit of mass/charge. I think this is a particularly difficult idea just because it is something that really never gets used in normal conversation other than with batteries. Let's be honest, very few people understand what potential means with batteries either. It is just a word that is used with very little context or understanding around it. We began talking about potential using contour maps and dealing with the grav. field. Potential can be seen as a hill. The steeper the hill the stronger the localized field is. The taller the hill, the more potential there is. It was easy to wrap our head around because most of us had seem something like this before. Electrical equipotentials were a bit more difficult. We have opposite charges now.
Grav energy = mgh Elec energy = qEd
Grav potential=energy/mass=gh Elec potential=energy/charge=Ed
At this point we did "the lab". I did not realize at the time how important this lab was, but we came back to it the rest of the workshop. Super important for our understanding. We placed two iron bars in a baking dish with a bit of water in it. We then connected them to a DC power source and used our potential-o-meters to measure the electrical potential at about a billion places. (Took forever!) we then graphed it using plot.ly to get a graph that looked just like a hill! 
We then used a phet simulator to see how this worked with point charges instead of plates. The hills did not seem to be constant around point charges. They looked more like this:The valley is caused by a negative charge as all positive charges would roll downhill towards it. Note that the hills change steepness as they get away from the charge. This goes back to the inverse square between distance and force on field strength. Interestingly, the inverse square thing doesn't seem to apply to the charged plates. We talked about this and the charges push on each other and pull on each other and based on superposition the forces stay pretty much equal. As you get farther from one plate you get closer to the other plate so it all stays constant.
This problem made my brain weak. At first glance it looks EXACTLY LIKE THE LAB WE DID!!!! So my lab group breezed through it. Then Don and Laura kept coming by and reminding us that they were not hooked up to a power supply in the problem.
Us: Yeah. We get it. (don't change anything because we are so amazingly right)
Them: But the power supply was keeping the potential constant.
Us: Yeah. Cool. No charges can leave or enter so.... We're good!
Them: Really?
Us: Yes?
Them: Really really?
Us: Look energy is increasing since the plates are being pulled away right? So the field strength should get smaller and the distance increases and so the potential stays the same. We. Are. Good! You are not going to get us with your Jedi Mind Tricks!
(They go away) Us in our group: Ok. Why do they keep asking us this. Are we doing something wrong? Potential has to be the same right? No charges can move! When plates move away we know the field gets smaller we saw it! So what could we be doing wrong?
Eventually we got back in a group and discussed this problem.Laura brought up this idea. If a charge is very close to one plate, pretty much only the charge next to it is pushing it away. All of the others are pushing on an oblique angle to it. Their forces balance out and so the charge gets pushed straight out from the plate. As the charge moves away the force from charge 3 gets reduced at the inverse square rate but here is where my mind exploded. At this point all of the charges around it have a greater effect because the angle they push at is much closer to 90! If you imagine the plate to be a huge wall (from a single charge perspective), the area of charges increases as a square to the distance! Yes, the one charge is less but the others start to help out more and so the force ends up being constant! Holy crap this changes everything! As the plates in question 11 separate the FIELD STAYS THE SAME!!!!!!!!! Energy goes up proportional to the distance moved. Since energy is equal to qEd and elec potential(V) is energy/q then Ee=qV. I can't believe we didn't see this before! If charge is not changing but energy is increasing, the potential CAN'T BE CONSTANT!!!!
Sorry for all the shouting. It was a very big moment for me in this unit.
Once we had this background set we were given these large blue cylinders that we were told were energy storage devices. (Later we learned they were called capacitors) A capacitor is basically two really big parallel plates rolled up into a smaller space but we could move the charges from one plate to another using a battery or a generator. (Note: This is not charging it! The device is still neutrally charged. Charges have just been moved from one plate to the other. We called this energized.)
There were various capacitors and we did a lab seeing how much energy was stored in each type. We found that as we increased the potential the energy increased as a square of the the change in the potential. The coefficient we labeled as 1/2 the capacitance. We then did a phet sim on capacitors to determine what things affect the capacitance. We also looked at using multiple capacitors. If we hooked them up in a straight line energy for each added capacitor went down! When we hooked them where one side was connected to one terminal of the battery and the other terminal to the other side (what we would later know as parallel) the graph of energy per capacitor added was linear! Crazy! As we thought about it it made some sense based on what we had done with the phet sim. Adding capacitors in parallel was like increasing the area of the plate which we saw had a direct relationship with energy. 2 capacitors = twice the area. For the one in series, the total potential was the same for all capacitors in a line so if there were 2 capacitors, each one only stored half the energy.
Saturday, July 16, 2016
Unit 1 Work Product (part 2) - 2016 E&M Modeling Instruction Workshop
To recap, go back and read the last post!
After this we came back to the pith ball and did an experiment. We hung the pith ball from 2 strings and wanted to see if there was a relationship between the distance two equally charged objects were brought together and the force between them. We charged the pith on a string and another pith on a stick with a fun fly stick. We then touched them together to be sure the charges on them were equal. We then slowly brought the stick pith toward the hanging pith. Since we knew the mass we could draw a force diagram to help us calculate the force of repulsion between the piths. See below.
The video of us taking data can be seen here. We used video and freeze frame to take our measurements. When we processed our data we found that the force seemed to increase at a square of the amount the distance decreased.
After that we went back to the lab and came up with a new equation:
Since each charge acts on each other charge it is a multiplication problem. (Top drawing has 4 charges on left and 2 charges on right. Each charge on the left feels a force from each charge on the right and vice versa. A weird thing though. In the bottom drawing where 6 charges are separated equally, 3 and 3, There is a repulsion of 9 arrows, where in the top drawing there is only 8 arrows. This is very interesting to me and I will need to think on it more. This has to be why Don had us touch the two pith balls together in the lab before taking measurements.)
After the discovery we began some of our deployments. The idea of conductors vs. Insulators came up. Especially on these problems:
After this we came back to the pith ball and did an experiment. We hung the pith ball from 2 strings and wanted to see if there was a relationship between the distance two equally charged objects were brought together and the force between them. We charged the pith on a string and another pith on a stick with a fun fly stick. We then touched them together to be sure the charges on them were equal. We then slowly brought the stick pith toward the hanging pith. Since we knew the mass we could draw a force diagram to help us calculate the force of repulsion between the piths. See below.
The video of us taking data can be seen here. We used video and freeze frame to take our measurements. When we processed our data we found that the force seemed to increase at a square of the amount the distance decreased.
We then discussed the experiment. Laura asked if only 1 electron transferred. Probably not. Probably millions. Which makes talking about charge difficult. It's like asking someone how far their Grandma lives away from them in inches! So scientists made up a unit for charge called the Coulomb. A coulomb is the charge of 6.25x10^18 electrons. Which means the charge of one proton or electron is 1.6x10^-19 C.
After that we went back to the lab and came up with a new equation:
Since the charge signs don't really match our idea of the signs we use for forces we decided to make it an absolute value. We also weren't sure if the charges should be multiplied or added at first. I looked at it like this:
Since each charge acts on each other charge it is a multiplication problem. (Top drawing has 4 charges on left and 2 charges on right. Each charge on the left feels a force from each charge on the right and vice versa. A weird thing though. In the bottom drawing where 6 charges are separated equally, 3 and 3, There is a repulsion of 9 arrows, where in the top drawing there is only 8 arrows. This is very interesting to me and I will need to think on it more. This has to be why Don had us touch the two pith balls together in the lab before taking measurements.)
Lastly our formula needs a proportionality constant because most equations need one. It is called k for obvious reasons (/sarcasm) and it's units are weird and make very little sense as an idea unlike many of the constants we have encountered thus far in physics.
The whole equation in all is called Coulomb's Law. It looks very similar to the Universal law of Gravitation. Wonder if that means something?
Saturday, July 2, 2016
Unit 1 Work Product - 2016 E&M Modeling Instruction Workshop
In order to obtain continuing education credit for this workshop I need to complete a "work product." The next few entries will be a part of that work product. Reflection is good for you anyway so I am happy to do it.
A very good discussion ensued. My takeaway is that an analogy is only useful if you as a learner creates it. I think it works that way because you can think of ways that the analogy fits and also ways that the analogy does NOT fit. As educators if we place an analogy into the minds of our students they may not intrinsically realize that the analogy has parts that do not work and may reinforce or even introduce incorrect thinking.
Laura rubbed a balloon on her hair and then stuck the balloon to the ceiling. We had to draw a force diagram for the forces on the balloon. Our original diagram looked like this:
We knew the balloon wasn't accelerating so the forces had to be balanced. But many others had a third force with the ceiling pushing down. We tried standing on chairs and looking to see if the balloon was deformed at the top but we couldn't really tell. Then Laura pulled the balloon down about 4 inches and let it go and it jumped back up to the ceiling!! Woah! So after that we discussed that the force upwards must be bigger than the force of the Earth pulling down so we made the change and added yet another ceiling force this time pushing down so that the forces were balanced.
The end result looked like this:
But how can the ceiling pull up and also push down? Since the balloon was pulled up without the ceiling touching it we concluded it must be some type of non-contact force. Some of my fellow students and I decided it must be some sort of static electricity force from the rubbing of the balloon. From prior knowledge we know this is most likely caused by the transfer of electrons from Laura's hair to the balloon or from the balloon to Laura's hair but we couldn't figure out a way to tell outside of just guessing. We also had some additional observations that as of yet are unexplained. The balloon only stuck to ceiling if the exact are Laura rubbed was placed near the ceiling. If we pointed the opposite side to the ceiling it did not stick. So it appears whatever is transferring stays in one location. Lastly, we didn't do anything to the ceiling so I'm not sure why're balloon stick to it and when we tried a balloon that was not rubbed it would not stick no matter what.
DAY 1 -
 |
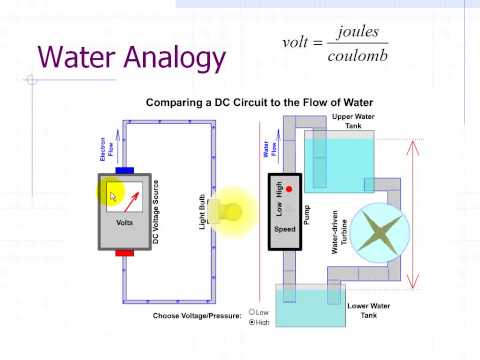| Totally makes sense now. |
We started by reading a very convoluted article that treated complicated topics in E&M as if they were really quite elementary and simple. As a class we pretty much disagreed with that point! Particular treatment was given to the use of analogies in physics in particular the analogy of electricity as water flowing in a hose.
We also had a lengthy discussion on the word "model". Model has a multitude of definitions that get bandied about in science education all the time. We talked for a very long time without getting to any real conclusion. I like the idea that a model is just something that exists in the mind of the student that helps them make sense of the world. That is model with a lowercase 'm'. The models that we build in modeling instruction are Models with an uppercase 'M'. That way we can distinguish if we are talking about a simple model or a complex one with many representations that give us a full picture of a particular phenomenon.
After that we actually started with learning about charges and entered into student mode. In student mode we try and put ourselves into the mindset of our students. What would they know going into the class? What questions would they have? What would they be thinking? It is much harder to do than many would realize.
Laura rubbed a balloon on her hair and then stuck the balloon to the ceiling. We had to draw a force diagram for the forces on the balloon. Our original diagram looked like this:
We knew the balloon wasn't accelerating so the forces had to be balanced. But many others had a third force with the ceiling pushing down. We tried standing on chairs and looking to see if the balloon was deformed at the top but we couldn't really tell. Then Laura pulled the balloon down about 4 inches and let it go and it jumped back up to the ceiling!! Woah! So after that we discussed that the force upwards must be bigger than the force of the Earth pulling down so we made the change and added yet another ceiling force this time pushing down so that the forces were balanced.
The end result looked like this:
But how can the ceiling pull up and also push down? Since the balloon was pulled up without the ceiling touching it we concluded it must be some type of non-contact force. Some of my fellow students and I decided it must be some sort of static electricity force from the rubbing of the balloon. From prior knowledge we know this is most likely caused by the transfer of electrons from Laura's hair to the balloon or from the balloon to Laura's hair but we couldn't figure out a way to tell outside of just guessing. We also had some additional observations that as of yet are unexplained. The balloon only stuck to ceiling if the exact are Laura rubbed was placed near the ceiling. If we pointed the opposite side to the ceiling it did not stick. So it appears whatever is transferring stays in one location. Lastly, we didn't do anything to the ceiling so I'm not sure why're balloon stick to it and when we tried a balloon that was not rubbed it would not stick no matter what.
Hoping to answer some of these questions over the course of the unit, Laura gave us a tool to use that might help us. We did an activity with Scotch tape. We had to layer 3 pieces of tape on the table like this:
We made two of these set-ups but always left the last piece on the table in case we needed to reset the other tapes. The 2 pieces on top were labeled top and bottom. When we pulled off the two top pieces and held them together they repelled each other! The closer they got together the more intensely they seemed to repel. Then we stuck the tapes back down on the stack. The second time we pulled the top and bottom tapes off the stack at the same time. Then we separated the tapes in the air. The top tapes still repelled each other but they attracted the bottom tapes. When two bottom tapes were brought together they repelled as well. (Pro-tip: when you first pull the tapes off of the table run your fingers down them before separating the two tapes. This makes them work better) Then a curious thing happened. Don had given us some strips of paper and Al foil. Both of those were attracted to the top AND the bottom tapes. This seemed weird because the paper and foil did not attract each other at all, so it seemed as if they had no charge.
After some discussion we decided that like charges seem to repel each other since tops repel tops and bottoms repel bottoms. And then opposite charged objects attract each other but so do a charged object and a neutral object. So the only way we can really know the charge of something is if they repel. If this happens we can 100% know the charges are the same.
To try and figure out what was happening in the neutral objects attracting we zoomed into the tapes on a micro level and imagined the plus and minus charges of atoms. The pluses are in the nucleus and can't move, but the minus charges are zooming around the outside. SO when a plus charged object comes near a neutral one, the pluses in the charged object push on the electrons which depending on the material can move a little to a lot.
You can see in the image from a pHet sim we used. The minus charges in the wall bend away from the charged balloon leaving more pluses behind which can't move. So the surface of the wall is more positively charged and so the opposite charged balloon sticks to it. (This sim has a slight issue. In our experiences the charged side of the balloon has to face the wall in order for this effect to work. The opposite side from where we charged the balloon will not stick. Charges don't easily move on an insulator which the rubber of the balloon apparently is. Conductors like metal can allow electrons to move freely.) The opposite effect happens if you bring a positive charged object toward a neutral object. In the picture if the balloon had a positive charge on it the electrons would move toward the balloon leaving a net negative charge on the surface of the wall and they would attract. We named this phenomenon Polarization.
We then played with Fun Fly sticks which through testing we discovered develop a positive charge on the end when you push a button. No clue how it works. We also used foam boards with rabbit fur to charge them and pie plates with a styrofoam cup to create an insulated handle. Last we had a pith ball hanging from a thread on an apparatus that Don called an electrophorus. A pith ball is a very light ball about the size of a marble. It has a silvery coating on it and is fairly easy to charge and discharge.
In the top picture, the pith ball is neutral (equal + and -). The positively charged fun fly stick is brought near it and then we touch the pith ball. Since the ball is near a positive charged object the - charges in the ball are attracted and move toward the fly stick side of the ball. This leaves a positively charged area on the backside of the ball. As my finger got near to the pith ball the same thing happens again in my finger. The - charges are attracted to the tip of my finger. When I touch the ball some of those - charges move onto the ball because they are attracted by the positive charges near the surface and repelled by the negatives in the tip of my finger. When I remove my finger and the fun fly stick, the ball now has an excess of - charges so is negatively charged. You can do this in reverse if you bring the balloon (negative charge) near the pith ball. The charges leave the ball and go into my finger instead of the other way around.
I have more yet to discuss but this post is getting very long so I will make a part 2!
 |
| pHet Simulation Balloons and Static Electricity |
But we still don't know what charge the tapes are. Is top a + charge? A - charge? Well, apparently, it is well-known that a glass rod rubbed with silk develops a + charge. So we used that to determine charges of things that we didn't know. Results are listed in the next picture:
R stands for repel and A attract. Remember that only repelling tells us anything for sure so looking at the chart, top tape and glass are the same charge (positive), and bottom tape and plastic are the same charge (negative). The silk didn't really seem to react to anything, but since the glass became positive, the silk had to have become negative. This is due to the idea of conservation of charge. If the glass is becoming positively charged that means that negative charges are being removed from it. They have to go somewhere and the only logical place would be on the item rubbing against it. So the rubber balloon became negative (repelled the bottom tape in testing) which means the fur or hair (human fur) must take on a positive charge.
We then played with Fun Fly sticks which through testing we discovered develop a positive charge on the end when you push a button. No clue how it works. We also used foam boards with rabbit fur to charge them and pie plates with a styrofoam cup to create an insulated handle. Last we had a pith ball hanging from a thread on an apparatus that Don called an electrophorus. A pith ball is a very light ball about the size of a marble. It has a silvery coating on it and is fairly easy to charge and discharge.
When you hold a charged object near the pith ball it attracts, but as soon as it touches the object it leaps away and then is repelled by it. We concluded that the pith ball must have had charges transferred to or from it through the contact. It didn't have a charge (attracted by polarization) then it did after it touched (same as the charged object that touched it.) To discharge the pith ball you touch it with your finger. We called this grounding. Evidently you can do this all day and not build up a charge yourself. We apparently have LOTS of electrons that we can donate or accept without changing our overall charge. Whereas the pith ball has very little mass and so the same number of electrons transferred is a large percentage of its overal charge.
We then did a weird thing with the pie plate. We charged a foam board and brought the pan close to, but not touching the foam. Then we touched the side of the pie pan and got a small shock. We removed the pan away from the foam and, upon testing, the pie pan had a positive charge! Then we touched the pan and again it gave a little shock and went back to being neutral. You could do this over and over and the foam didn't seem to ever lose charge. We drew out some representations of what we thought were happening to the charges and after discussion came up with this idea:
In the top picture, the pith ball is neutral (equal + and -). The positively charged fun fly stick is brought near it and then we touch the pith ball. Since the ball is near a positive charged object the - charges in the ball are attracted and move toward the fly stick side of the ball. This leaves a positively charged area on the backside of the ball. As my finger got near to the pith ball the same thing happens again in my finger. The - charges are attracted to the tip of my finger. When I touch the ball some of those - charges move onto the ball because they are attracted by the positive charges near the surface and repelled by the negatives in the tip of my finger. When I remove my finger and the fun fly stick, the ball now has an excess of - charges so is negatively charged. You can do this in reverse if you bring the balloon (negative charge) near the pith ball. The charges leave the ball and go into my finger instead of the other way around.I have more yet to discuss but this post is getting very long so I will make a part 2!
Thursday, June 23, 2016
The story so far...
So I have not blogged in a very long time. At least not on this blog. I feel I was a better teacher when I did, but life has been very crazy as of late (and by this I mean the last like 4 years.) But I'd like to get back into it. Reflection is crucial to improving yourself. Plus I have some ideas that have been percolating that I'd like to share. But that is for later this summer. After many summers of leading other teachers to the wonders of modeling instruction I finally get to go back as a participant this year with the E&M workshop. I could not be more excited for it. We are only 3 days in and already so many good things have come from it. I am currently working on the first unit summary and will be posting it soon after we are finished with the unit. I have a feeling we will be finishing it tomorrow or Monday at the latest. I have used many of the modeling materials for this unit before, but nowhere near as coherently. Very good stuff.
Tuesday, July 8, 2014
Standards Based Grading: A primer
So every year during the modeling workshop the question of grading comes up. I think it is a natural question because this teaching method is fundamentally different from what most of us have done before. A lot of the onus of the learning is placed upon the kids. They need to construct their own understanding from their experiences in class. This can be problematic because since our students come from different backgrounds (experiences, math abilities, reasoning abilities, etc.) it is ridiculous to think that they all reach understanding at the same time. So how do we handle this? How do we tell our students that it is ok to make mistakes and yet not have a grading system that allows for this?
Grading has always been a particular beef for me and I am sure like most of you, your grading system is eerily similar to a teacher you once had. The problem is that I think many of us never considered what our grades actually mean? What does a C on a quiz tell a student? How do you handle that question at a parent-teacher conference? If you are like me you probably have said, "Your student just needs to study more." Really? Does that actually help? What do I need to study? I need a study guide! As a student that doesn't really help me. And it leads to the the obvious conclusion that many students have.. "I'm not a good test taker." And while some students legitimately have test anxiety issues I would guess an enormous majority of the students who say this do not. They just don't understand the material.
So wouldn't it be nice to give them something specific to work on? If you told a student that the reason they got a C on a quiz is because they had difficulty interpreting a position vs. time graph. Now they have a direction. It is an actionable statement. And in my mind it is much preferred for both student and parent. These are the things that you get from your elementary student's teacher. Billy needs to work on his alphabet letters. Susan needs to practice her addition facts. This is something you can work with. Secondary grades? Not so much.
So I made the switch to Standards Based Grading. Not without a bunch of bumps in the road but it is definitely a trip that I have found rewarding as have my students. Much like physics modeling instruction there is not a "right one way" to do SBG. And you will find lots of resources for it. The main page that started me on this road are Think Thank Thunk by Shawn Cornally. He has several others that he links to on his page that I recommend checking out. I warn you though...
There are as many styles of SBG as there are traditional grading systems so I am sure you can find some to your liking. There are even some that are a hybrid of traditional and SBG together that I have seen. But no matter, SBG shifts the discussion from "What's my grade?" to "What do I need to work on to learn this?" It is a huge difference. Everyone can get an A as long as they master the standards.
So how does it look in my classroom?
I give the students a list of the unit standards at the beginning of the unit. I then give a series of short quizzes that spiral and build off each other. Each one tests anywhere from 3-5 standards usually. I score each standard on a 3 point scale (some would argue 4). A 3 means mastery of the standard. A 2 shows some understanding but with some mistakes. A 1 shows little understanding at all. A 0 is if they didn't take the assessment. When we are in the unit, most standards will get retested several times. If most of the students grasp the concept I will take it off the next quiz. If they struggle I will put questions on the next assessment for that standard. At no time is learning off limits to my students. So even if we are on Unit 4 and students are still working with Unit 1 standards, they can still retest those standards. If it is the next quarter I still let the students work on standards from the previous quarter. Even though this leads to more paperwork for me in regards to grade change forms, etc, they are worth it in my opinion because it reinforces the idea that it is ok in my class to make mistakes.
This change is hard for many of your students, but especially for your "Best" students. You know, the ones who have learned the game of school. Memorize, regurgitate, repeat. Nothing matters but the grade. Suddenly changing the rules on them is very difficult for them. They will need lots of reassurance and help but I have found all but the most entrenched are eventually converted. This is also challenging for many parents as they will not understand what you are trying to do and sometimes the message that comes home is not the best (see students referenced early in this paragraph.) I have found that having a script ready helps a lot for the parent contacts that are inevitable. As I have continued to use this method I have found parent phone calls have reduced as word has spread and on whole my students really grow to like this because they feel like they are actually accomplishing something. They are learning and they have proof.
I hope this helps. If you are not familiar with Rick Wormeli, you should be. Here are some of his youtube videos. Feel free to comment any questions you have!
Grading has always been a particular beef for me and I am sure like most of you, your grading system is eerily similar to a teacher you once had. The problem is that I think many of us never considered what our grades actually mean? What does a C on a quiz tell a student? How do you handle that question at a parent-teacher conference? If you are like me you probably have said, "Your student just needs to study more." Really? Does that actually help? What do I need to study? I need a study guide! As a student that doesn't really help me. And it leads to the the obvious conclusion that many students have.. "I'm not a good test taker." And while some students legitimately have test anxiety issues I would guess an enormous majority of the students who say this do not. They just don't understand the material.
 |
| I'll do the math for you... All of these students would get the same grade for the course. Does this seem right? |
So wouldn't it be nice to give them something specific to work on? If you told a student that the reason they got a C on a quiz is because they had difficulty interpreting a position vs. time graph. Now they have a direction. It is an actionable statement. And in my mind it is much preferred for both student and parent. These are the things that you get from your elementary student's teacher. Billy needs to work on his alphabet letters. Susan needs to practice her addition facts. This is something you can work with. Secondary grades? Not so much.
So I made the switch to Standards Based Grading. Not without a bunch of bumps in the road but it is definitely a trip that I have found rewarding as have my students. Much like physics modeling instruction there is not a "right one way" to do SBG. And you will find lots of resources for it. The main page that started me on this road are Think Thank Thunk by Shawn Cornally. He has several others that he links to on his page that I recommend checking out. I warn you though...
 |
| Woah. -Keanu Reeves |
There are as many styles of SBG as there are traditional grading systems so I am sure you can find some to your liking. There are even some that are a hybrid of traditional and SBG together that I have seen. But no matter, SBG shifts the discussion from "What's my grade?" to "What do I need to work on to learn this?" It is a huge difference. Everyone can get an A as long as they master the standards.
So how does it look in my classroom?
I give the students a list of the unit standards at the beginning of the unit. I then give a series of short quizzes that spiral and build off each other. Each one tests anywhere from 3-5 standards usually. I score each standard on a 3 point scale (some would argue 4). A 3 means mastery of the standard. A 2 shows some understanding but with some mistakes. A 1 shows little understanding at all. A 0 is if they didn't take the assessment. When we are in the unit, most standards will get retested several times. If most of the students grasp the concept I will take it off the next quiz. If they struggle I will put questions on the next assessment for that standard. At no time is learning off limits to my students. So even if we are on Unit 4 and students are still working with Unit 1 standards, they can still retest those standards. If it is the next quarter I still let the students work on standards from the previous quarter. Even though this leads to more paperwork for me in regards to grade change forms, etc, they are worth it in my opinion because it reinforces the idea that it is ok in my class to make mistakes.
This change is hard for many of your students, but especially for your "Best" students. You know, the ones who have learned the game of school. Memorize, regurgitate, repeat. Nothing matters but the grade. Suddenly changing the rules on them is very difficult for them. They will need lots of reassurance and help but I have found all but the most entrenched are eventually converted. This is also challenging for many parents as they will not understand what you are trying to do and sometimes the message that comes home is not the best (see students referenced early in this paragraph.) I have found that having a script ready helps a lot for the parent contacts that are inevitable. As I have continued to use this method I have found parent phone calls have reduced as word has spread and on whole my students really grow to like this because they feel like they are actually accomplishing something. They are learning and they have proof.
I hope this helps. If you are not familiar with Rick Wormeli, you should be. Here are some of his youtube videos. Feel free to comment any questions you have!
Monday, June 30, 2014
Days 3,4,5 SEMiModPhys14: Why three days in one?
Answer: I'm lame.
These last three days have been difficult for me. I have been worried that we aren't making the impact that I have been hoping for. Are the participants getting the same transformative experience I got? Just wait.. Be patient.. But it is so hard.
I think it is starting to happen though and I think the Hammer and Mestre articles helped a lot. Comments and questions have subtly been changing from the "I don't know if this will work" variety to more in line with "How will I make this work?" That is a huge step in my mind. There are many who I know will never go back. Others that are on the fence and a few who I think still need some time to process everything.
One of the biggest hang-ups I think some people are still having is the question of student buy-in. How will you get your students to fundamentally change to where they accept this radical change where you have removed the spoon from their mouths? It is not easy for some. But I think most crave this style of education. They just don't know it. So how do you build this culture of cooperative student learning? For me, culture building is another aspect of my class. Do I get preachy at times? Yep. Do I tell them repeatedly that I have utmost confidence in their physics and science abilities? Yep. Do I actually believe that? Yep. And I think that is the difference right there. I truly think that EVERY kid that comes into my classroom will learn physics. They may not get a perfect score on the FCI when I'm done. (Did I just say may?) But they will learn. And they will have fun doing it. And they will ask me to give them homework. Even though it is not graded. Ever.
Crazy right? No. It's not. It happens. And not just with my IB students. It happened in the normal high school I taught at as well. Students want to learn. They want to be challenged. They want to be told they can fail and you will still admire, love and respect them. And I do. It's not rocket surgery people.
I guess this goes for my students this summer too. No matter what the outcome, I know they will go back into their classrooms changed from the experience this summer. I know they will think about their student's understanding. I know they will try and probe for misconceptions and work to correct these to create a better conceptual foundation for what they teach. So I guess I've already made that difference I was hoping for, and I haven't even showed them my bowling ball lab.
These last three days have been difficult for me. I have been worried that we aren't making the impact that I have been hoping for. Are the participants getting the same transformative experience I got? Just wait.. Be patient.. But it is so hard.
I think it is starting to happen though and I think the Hammer and Mestre articles helped a lot. Comments and questions have subtly been changing from the "I don't know if this will work" variety to more in line with "How will I make this work?" That is a huge step in my mind. There are many who I know will never go back. Others that are on the fence and a few who I think still need some time to process everything.
One of the biggest hang-ups I think some people are still having is the question of student buy-in. How will you get your students to fundamentally change to where they accept this radical change where you have removed the spoon from their mouths? It is not easy for some. But I think most crave this style of education. They just don't know it. So how do you build this culture of cooperative student learning? For me, culture building is another aspect of my class. Do I get preachy at times? Yep. Do I tell them repeatedly that I have utmost confidence in their physics and science abilities? Yep. Do I actually believe that? Yep. And I think that is the difference right there. I truly think that EVERY kid that comes into my classroom will learn physics. They may not get a perfect score on the FCI when I'm done. (Did I just say may?) But they will learn. And they will have fun doing it. And they will ask me to give them homework. Even though it is not graded. Ever.
Crazy right? No. It's not. It happens. And not just with my IB students. It happened in the normal high school I taught at as well. Students want to learn. They want to be challenged. They want to be told they can fail and you will still admire, love and respect them. And I do. It's not rocket surgery people.
I guess this goes for my students this summer too. No matter what the outcome, I know they will go back into their classrooms changed from the experience this summer. I know they will think about their student's understanding. I know they will try and probe for misconceptions and work to correct these to create a better conceptual foundation for what they teach. So I guess I've already made that difference I was hoping for, and I haven't even showed them my bowling ball lab.
Subscribe to:
Posts (Atom)